II. Logistic regression

0. Presentation

Idea: classify $y=0$ (negative class) or $y=1$ (positive class)

From linear regression $h_\theta(x) = \theta^TX$ We need to choose hypothesis function such as $0 \leq h(x) \leq 1$

1. Hypothesis function

$h_{\theta }\left(x\right)=g\left({\sum }_{i=0}^n{\theta }_i{x}_i\right)\text{<mi mathvariant="normal">f</mi><mi mathvariant="normal">o</mi><mi mathvariant="normal">r</mi>}g\left(z\right)=\frac{1}{1+e^{-z}}$
h\theta(x) = g(\sum{i=0}^{n}\theta_ix_i) \quad \textrm{for} \quad g(z) = \frac{1}{1 + e^{-z}}

Notes: Octave implementation of sigmoid function

g = 1 ./ ( 1 + e .^ (-z));

Vectorized form:
Since $\sum_{i=0}^{n}\theta_ix$i = \theta^TX. The vectorized form of $h\theta(x)$ is

$\frac{1}{1+e^{-{\theta }^{T}X}}\text{<mi mathvariant="normal">o</mi><mi mathvariant="normal">r</mi>}sigmoid\left({\theta }^{T}X\right)$
\frac{1}{1 + e^{-\theta^TX}} \quad \textrm{or} \quad sigmoid(\theta^TX)

Octave implementation

h = sigmoid(theta' *  X)

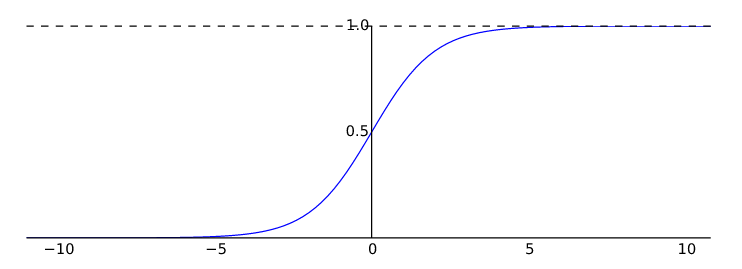
$h(x)$ is the estimate probability that $y=1$ on input $x$

When $sigmoid(\theta^TX) \geq 0.5$ then we decide $y=1$. As we know $sigmoid(\theta^TX) \geq 0.5$ when $\theta^TX \geq 0$

So for $y=1$ , $\theta^TX \geq 0$. We call $\theta^TX$ is the line that define the Decision boundary that separate the area where $y=0$ and $y=1$. It does not need to be linear since X can contain polynomial term.

Decision boundary is the property of the hypothesis and parameter $\theta$, not of the training set

2. The cost function

We need to choose the cost function so that it is “convex” toward one single global minimum

Cost function

$\begin{array}{cc}& J_{\left(\theta \right)}=\frac{1}{m}{\sum }_{i=1}^{m}Cost\left(h_{\theta }\right(x^{\left(i\right)},y^{\left(i\right)}\left)\right)\\ & \text{<mi mathvariant="normal">w</mi><mi mathvariant="normal">i</mi><mi mathvariant="normal">t</mi><mi mathvariant="normal">h</mi>}\\ & Cost\left(h_{\theta }\right(x^{\left(i\right)},y^{\left(i\right)}\left)\right)=\{\begin{array}{ccc}-log\left(h_{\theta }\right(x\left)\right)& \text{<mi mathvariant="normal">i</mi><mi mathvariant="normal">f</mi>}& y=1\\ -log(1-h_{\theta }(x\left)\right)& \text{<mi mathvariant="normal">i</mi><mi mathvariant="normal">f</mi>}& y=0\end{array}\end{array}$
\begin{aligned}
&J{(\theta)} = \frac{1}{m} \sum{i=1}^{m}Cost( h\theta(x^{(i)}, y ^ {(i)})) \
&\textrm{with} \quad \
&Cost( h\theta(x^{(i)}, y ^ {(i)})) =
\left{
\begin{array}{c}
-log(h\theta(x))&\text{if} &y = 1 \
-log(1 - h\theta(x))&\text{if} &y = 0
\end{array}
\right.
\end{aligned}

A simplified form of the cost function is:
$J_{\left(\theta \right)}=-\frac{1}{m}\left[{\sum }_{i=1}^m{y}^{\left(i\right)}log\right(h_{\theta }\left(x^{\left(i\right)}\right)+(1-y^{\left(i\right)})log(1-h_{\theta }(x^{\left(i\right)}\left)\right)]$
J{(\theta)} = -\frac{1}{m}\left[ \sum{i=1}^{m} y^{(i)} log(h\theta(x^{(i)}) + (1-y^{(i)})log(1 - h\theta(x^{(i)}))\right]

Vectorized form:
$J_{\left(\theta \right)}=\frac{1}{m}(-y^{T}log(sigmoid\left(X\theta \right))-(1-y^T\left)log\right(1-sigmoid\left(X\theta \right)\left)\right)$
J_{(\theta)} = \frac{1}{m}(-y^Tlog(sigmoid(X\theta)) - (1-y^T)log(1-sigmoid(X\theta)))

Code in Octave to compute cost function

J = (1/m) * ( -y' * log(sigmoid(X*theta) ) - (1-y') * log(1-sigmoid(X*theta)) );

We need to get the parameter $\theta$ where $J${(\theta)} is min. Then we can make a prediction when given new $x$ using
$h_{\theta }\left(x\right)=\frac{1}{1+e^{-{\theta }^{T}X}}$
h\theta(x) = \frac{1}{1 + e^{-\theta^TX}}

3. Gradient Descent algorithm

Using Gradient Descent to find value of $\theta$ when $J_{(\theta)}$ is min, we have

Repeat until convergence
${\theta }_j:={\theta }_j-\alpha \frac{\mathrm{\partial }}{\mathrm{\partial }{\theta }_j}J\left(\theta \right)$
\theta_j := \theta_j - \alpha \frac {\partial }{\partial \theta_j}J(\theta)

Repeat until convergence
${\theta }_j:={\theta }_j-\alpha \frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})x^{\left(i\right)}$
\theta_j := \thetaj - \alpha \frac{1}{m} \sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) x^{\left(i\right)}

Vectorized form:
$\theta :=\theta -\frac{\alpha }{m}\left(X^T\right(sigmoid\left(X\theta \right)-\vec{y}\left)\right)$
\theta := \theta - \frac{\alpha}{m} \left( X^T (sigmoid(X\theta) - \vec{y}) \right)

Code in Octave to compute gradient step $\frac {\partial }{\partial \theta_j}J(\theta)$

grad = (1 / m) * (X' * (sigmoid( X * theta) - y) );

4. Adding Regularization parameter

Regularized cost function:
$J_{\left(\theta \right)}=-\frac{1}{m}\left[{\sum }_{i=1}^m{y}^{\left(i\right)}log\right(h_{\theta }\left(x^{\left(i\right)}\right)+(1-y^{\left(i\right)})log(1-h_{\theta }(x^{\left(i\right)}\left)\right)]+\frac{\lambda }{2m}{\sum }_{j=1}^n{\theta }_j^2$
J{(\theta)} = -\frac{1}{m}\left[ \sum{i=1}^{m} y^{(i)} log(h\theta(x^{(i)}) + (1-y^{(i)})log(1 - h\theta(x^{(i)}))\right] + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2

The second sum, $\sum_{j=1}^{n}\theta_j^2$ means to explicitly exclude the bias term, $\theta_0$. I.e. the $\theta$ vector is indexed from 0 to n (holding n+1 values, $\theta_0$ through $\theta_n$), and this sum explicitly skips $\theta_0$, by running from 1 to n, skipping 0.

Octave code to compute cost function with regularization

J = (1/m) * (-y' * log(sigmoid(X*theta)) - (1-y')*log(1-sigmoid(X*theta))) + lambda/(2*m)*sum(theta(2:end).^2);

Thus, when computing the equation, we should continuously update the two following equations:
Regularized Gradient Descent:
Repeat
{
$\begin{array}{cc}{\theta }_0& :={\theta }_0-\alpha \frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})x_0^{\left(i\right)}\\ {\theta }_j& :={\theta }_j-\alpha [\left(\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})x^{\left(i\right)}\right)+\frac{\lambda }{m}{\theta }_j]\text{<mi mathvariant="normal">f</mi><mi mathvariant="normal">o</mi><mi mathvariant="normal">r</mi>}j\ge 1\end{array}$
\begin{aligned}
\theta_0 &:= \theta0 - \alpha \frac{1}{m} \sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) x_0^{\left(i\right)} \
\theta_j &:= \thetaj - \alpha \left[ \left(\frac{1}{m} \sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) x^{\left(i\right)} \right) + \frac{\lambda}{m}\theta_j \right] \quad \textrm{for} \quad j \geq 1
\end{aligned}

}

Octave code to compute gradient step $\frac {\partial }{\partial \theta_j}J(\theta)$

grad = (1 / m) * (X' * (sigmoid( X * theta) - y)) + (lambda/m)*[0; theta(2:end)];

Notice that we don’t add the regularization term for $\theta_0$

5. Advanced Optimization

Prepare a function that can compute $J_{(\theta)}$ and $\frac {\partial }{\partial \theta_j}J(\theta)$ for a given $\theta$

function [jVal, gradient] = costFunction(theta)
  jVal = [...code to compute J(theta)...];
  gradient = [...code to compute derivative of J(theta)...];
end

Then with this function Octave can provide us some advanced algorithms to compute min of $J_{(\theta)}$. We should not implement these below algorithms by ourselves.

• Conjugate gradient
• BFGS
• L-BFGS

options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

We give to the function fminunc() our cost function, our initial vector of theta values, and the options object that we created beforehand.

Advantages:
No need to pick up $\alpha$.
Often faster than gradient descent.

Disadvantages:
More complex.
Practical advice: try a couple of different libraries.

I. Linear regression

0. Presentation

Idea: try to fit the best line to the training sets

1. Hypothesis function

$\begin{array}{cc}{h}_{\theta }\left(x\right)& ={\theta }_0+{\theta }_1{x}_1+{\theta }_2{x}_2+\mathrm{.}\mathrm{.}\mathrm{.}\\ & ={\sum }_{i=0}^n{\theta }_i{x}_i\end{array}$
\begin{aligned}
h_\theta(x) & = \theta_0 + \theta_1x_1 + \theta_2x2 + … \
& = \sum{i=0}^{n}\theta_ixi
\end{aligned}

Vectorized form:
$h_{\theta }\left(x\right)=\left[\begin{array}{cccc}{\theta }_0& {\theta }_1& {\theta }_2& \mathrm{.}\mathrm{.}\mathrm{.}\end{array}\right]\left[\begin{array}{c}{x}_0\\ x_1\\ x_2\\ \mathrm{.}\mathrm{.}\mathrm{.}\end{array}\right]={\theta }^{T}X$
h\theta(x) = \left[\begin{matrix} \theta_0 & \theta_1 & \theta_2 & … \end{matrix}\right] \left[\begin{matrix} x_0 \ x_1 \ x_2 \ … \end{matrix}\right] = \theta^TX

Octave implemtation
Prepping by adding an all-one-column in front of X for $x_0$

h = theta' * X

The line fits best when the distance of our hypothesis to the sample training set is minimum.

Distance from hypothesis to the training set $h_\theta(x) -y = \theta_0 + \theta_1x_1 + \theta_2x_2 + … - y$

2. The cost function

Do the above for every sample point we arrive at the cost function below (or square error function or mean squared error)

$J_{\left(\theta \right)}=\frac{1}{2m}{\sum }_{i=1}^m{\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})}^2$
J{(\theta)} = \frac{1}{2m}\sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) ^ 2

Octave implementation

J = 1 / (2*m) * sum((X * theta - y).^2)

Vectorized form:

$J_{\left(\theta \right)}=\frac{1}{2m}(X\theta -\vec{y}{)}^T(X\theta -\vec{y})$
J_{(\theta)} = \frac{1}{2m}(X\theta - \vec{y}) ^ T ( X\theta - \vec{y})

J = 1 / (2*m) * (X*theta - y)' * (X*theta - y);

3. Batch Gradient Descent algorithm

To find out the value of $\theta$ when $J_{(\theta)}$ is min, we can use batch Gradient descent rule below:

Repeat until convergence
${\theta }_j:={\theta }_j-\alpha \frac{\mathrm{\partial }}{\mathrm{\partial }{\theta }_j}J\left(\theta \right)$
\theta_j := \theta_j - \alpha \frac {\partial }{\partial \theta_j}J(\theta)

and if we take the partial derivative of $J_{(\theta)}$ respect to $\theta_j$ we have:
Repeat until convergence
${\theta }_j:={\theta }_j-\alpha \frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})x^{\left(i\right)}$
\theta_j := \thetaj - \alpha \frac{1}{m} \sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) x^{\left(i\right)}

Octave implementation

for feature = 1:size(X, 2)
  theta(feature) = theta(feature) - alpha*(1/m) * sum((X*theta-y) .* X(:,feature));
end

Vectorized form:
$\theta :=\theta -\frac{\alpha }{m}\left(X^T\right(X\theta -\vec{y}\left)\right)$
\theta := \theta - \frac{\alpha}{m} \left( X^T (X\theta - \vec{y}) \right)

Octave implementation

theta = theta - alpha*(1/m) * (X' * (X*theta-y));

Notes on using gradient descent

Gradient descent need many iteration and works well for number of features n > 10,000

Complexity of $O(n^2)$

Choosing alpha:
Should step 0.1, 0.3, 0.6, 1 …

Feature normalization
To make gradient descent converges faster we can normalize the data a bit
$x_i=\frac{x_i-{\mu }_i}{s_i}$
x_i = \frac{x_i - \mu_i}{s_i}

where mu_i is the average of all the value of feature i
s_i is the range of value or the standard deviation of feature i

After having theta, we can plug X and theta back in hypothesis function to find out the prediction
$h_\theta(x) = \theta^TX$

4. Adding Regularization parameter

Why Regularization ?
The more features introduced, the higher chances that overfitting happens. To address overfitting, we can reduce the number of features or use regularization:

• Keep all the features, but reduce the magnitude of parameters θj.
• Regularization works well when we have a lot of slightly useful features.

How? Adding regularization parameter changing:

Regularized cost function:
$J_{\left(\theta \right)}=\frac{1}{2m}[{\sum }_{i=1}^m{\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})}^2+\lambda {\sum }_{j=1}^n{\theta }_j^2]$
J{(\theta)} = \frac{1}{2m} \left [ \sum{i=1}^{m} \left( h\theta ( x^{(i)} ) - y^{(i)} \right) ^ 2 + \lambda \sum{j=1}^{n}\theta_j^2 \right]

Regularized Gradient Descent:

We will modify our gradient descent function to separate out $\theta_0$ from the rest of the parameters because we do not want to penalize $\theta_0$.

Repeat
{
$\begin{array}{cc}{\theta }_0& :={\theta }_0-\alpha \frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})x_0^{\left(i\right)}\\ {\theta }_j& :={\theta }_j-\alpha [\left(\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})x^{\left(i\right)}\right)+\frac{\lambda }{m}{\theta }_j]\text{<mi mathvariant="normal">f</mi><mi mathvariant="normal">o</mi><mi mathvariant="normal">r</mi>}j\ge 1\end{array}$
\begin{aligned}
\theta_0 &:= \theta0 - \alpha \frac{1}{m} \sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) x_0^{\left(i\right)} \
\theta_j &:= \thetaj - \alpha \left[ \left( \frac{1}{m} \sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) x^{\left(i\right)} \right) + \frac{\lambda}{m}\theta_j \right] \quad \textrm{for} \quad j \geq 1
\end{aligned}

}

5. Normal equation

There is another way to minimize $J_{(\theta)}$. This is the explicitly way to compute value of $\theta$ without resorting to an iterative algorithm.
$\theta =(X^{T}X{)}^{-1}{X}^T\vec{y}$
\theta = (X^TX)^{-1} X^T\vec{y}

Sometimes $(X^TX)$ is non-invertable. Some of the reasons include existence of redundant features or too many features $(m \leq n)$. We should recude number of feature or switch to gradient descent in such case.

Octave implementation

theta = (X' * X)^(-1) * X' * y;

Notes on using Normal equation

No need to choose alpha.

No need to run many iterations.

Feature scaling is also not necessary.

Complexity of $O(n^3)$ since we need to calculate inverse of $(X^TX)$ or pinv(X'* X)

Close of n is very large, should switch to gradient descent.

We can also apply regularization to the normal equation
$\begin{array}{cc}& \theta =(X^{T}X+\lambda \cdot L{)}^{-1}{X}^T\vec{y}\\ & \text{<mi mathvariant="normal">w</mi><mi mathvariant="normal">i</mi><mi mathvariant="normal">t</mi><mi mathvariant="normal">h</mi>}L=\left[\begin{array}{ccccc}0& & & & \\ & 1& & & \\ & & 1& & \\ & & & \ddots & \\ & & & & 1\end{array}\right]\end{array}$
\begin{aligned}
&\theta = (X^TX+ \lambda \cdot L)^{-1} X^T\vec{y} \
&\textrm{with} \quad L = \begin{bmatrix}
0 & & & &\
& 1 & & & \
& & 1 & & \
& & & \ddots & \
& & & & 1
\end{bmatrix}
\end{aligned}

Recall that if $m < n$, and may be non-invertible if $m = n$ then $X^TX$ is non-invertible. However, when we add the term $\lambda \cdot L$, then $X^TX + \lambda \cdot L$ becomes invertible.

Machine Leaning

2 definitions:

Arthur Samuel

the field of study that gives computers the ability to learn without being explicitly programmed.

Tom Mitchell:

A computer program is said to learn from experience E with respect to some class of tasks T and performance measure P, if its performance at tasks in T, as measured by P, improves with experience E.

General notations

• m = Number of training examples.
• n = Number of features.
• x = Input variables.
• y = Output variables.
• (x,y) = one training example.
• x(i), y(i) = i(th) training example.
• h = hypothesis function, h maps from x’s to y’s.

1. Supervised Learning

In supervised learning, we are given a data set and already know what our correct output should look like, having the idea that there is a relationship between the input and the output.

Supervised learning problems are categorized into “regression” and “classification” problems. In a regression problem, we are trying to predict results within a continuous output, meaning that we are trying to map input variables to some continuous function. In a classification problem, we are instead trying to predict results in a discrete output. In other words, we are trying to map input variables into discrete categories.

2. Unsupervised Learning

Unsupervised learning allows us to approach problems with little or no idea what our results should look like. We can derive structure from data where we don’t necessarily know the effect of the variables.

We can derive this structure by clustering the data based on relationships among the variables in the data.

With unsupervised learning there is no feedback based on the prediction results.

Unsupervised learning problems are categorized into “clustering” and “non-clustering” problems.

Clustering: Take a collection of 1,000,000 different genes, and find a way to automatically group these genes into groups that are somehow similar or related by different variables, such as lifespan, location, roles, and so on.

Non-clustering: The “Cocktail Party Algorithm”, allows you to find structure in a chaotic environment. (i.e. identifying individual voices and music from a mesh of sounds at a cocktail party).