Machine Learning class note 3 - Logistic Regression

II. Logistic regression

0. Presentation

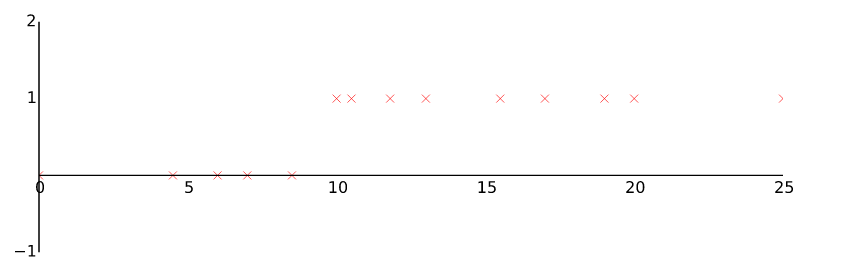
Idea: classify $y=0$ (negative class) or $y=1$ (positive class)

From linear regression $h_\theta(x) = \theta^TX$ We need to choose hypothesis function such as $0 \leq h(x) \leq 1$

1. Hypothesis function

$h_{\theta }\left(x\right)=g\left({\sum }_{i=0}^n{\theta }_i{x}_i\right)\text{<mi mathvariant="normal">f</mi><mi mathvariant="normal">o</mi><mi mathvariant="normal">r</mi>}g\left(z\right)=\frac{1}{1+e^{-z}}$
h\theta(x) = g(\sum{i=0}^{n}\theta_ix_i) \quad \textrm{for} \quad g(z) = \frac{1}{1 + e^{-z}}

Notes: Octave implementation of sigmoid function

g = 1 ./ ( 1 + e .^ (-z));

Vectorized form:
Since $\sum_{i=0}^{n}\theta_ix$i = \theta^TX. The vectorized form of $h\theta(x)$ is

$\frac{1}{1+e^{-{\theta }^{T}X}}\text{<mi mathvariant="normal">o</mi><mi mathvariant="normal">r</mi>}sigmoid\left({\theta }^{T}X\right)$
\frac{1}{1 + e^{-\theta^TX}} \quad \textrm{or} \quad sigmoid(\theta^TX)

Octave implementation

h = sigmoid(theta' *  X)

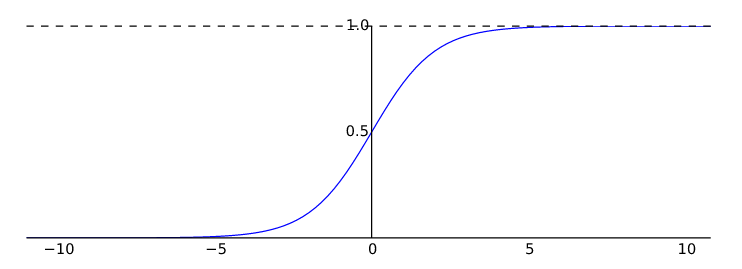
$h(x)$ is the estimate probability that $y=1$ on input $x$

When $sigmoid(\theta^TX) \geq 0.5$ then we decide $y=1$. As we know $sigmoid(\theta^TX) \geq 0.5$ when $\theta^TX \geq 0$

So for $y=1$ , $\theta^TX \geq 0$. We call $\theta^TX$ is the line that define the Decision boundary that separate the area where $y=0$ and $y=1$. It does not need to be linear since X can contain polynomial term.

Decision boundary is the property of the hypothesis and parameter $\theta$, not of the training set

2. The cost function

We need to choose the cost function so that it is “convex” toward one single global minimum

Cost function

$\begin{array}{cc}& J_{\left(\theta \right)}=\frac{1}{m}{\sum }_{i=1}^{m}Cost\left(h_{\theta }\right(x^{\left(i\right)},y^{\left(i\right)}\left)\right)\\ & \text{<mi mathvariant="normal">w</mi><mi mathvariant="normal">i</mi><mi mathvariant="normal">t</mi><mi mathvariant="normal">h</mi>}\\ & Cost\left(h_{\theta }\right(x^{\left(i\right)},y^{\left(i\right)}\left)\right)=\{\begin{array}{ccc}-log\left(h_{\theta }\right(x\left)\right)& \text{<mi mathvariant="normal">i</mi><mi mathvariant="normal">f</mi>}& y=1\\ -log(1-h_{\theta }(x\left)\right)& \text{<mi mathvariant="normal">i</mi><mi mathvariant="normal">f</mi>}& y=0\end{array}\end{array}$
\begin{aligned}
&J{(\theta)} = \frac{1}{m} \sum{i=1}^{m}Cost( h\theta(x^{(i)}, y ^ {(i)})) \
&\textrm{with} \quad \
&Cost( h\theta(x^{(i)}, y ^ {(i)})) =
\left{
\begin{array}{c}
-log(h\theta(x))&\text{if} &y = 1 \
-log(1 - h\theta(x))&\text{if} &y = 0
\end{array}
\right.
\end{aligned}

A simplified form of the cost function is:
$J_{\left(\theta \right)}=-\frac{1}{m}\left[{\sum }_{i=1}^m{y}^{\left(i\right)}log\right(h_{\theta }\left(x^{\left(i\right)}\right)+(1-y^{\left(i\right)})log(1-h_{\theta }(x^{\left(i\right)}\left)\right)]$
J{(\theta)} = -\frac{1}{m}\left[ \sum{i=1}^{m} y^{(i)} log(h\theta(x^{(i)}) + (1-y^{(i)})log(1 - h\theta(x^{(i)}))\right]

Vectorized form:
$J_{\left(\theta \right)}=\frac{1}{m}(-y^{T}log(sigmoid\left(X\theta \right))-(1-y^T\left)log\right(1-sigmoid\left(X\theta \right)\left)\right)$
J_{(\theta)} = \frac{1}{m}(-y^Tlog(sigmoid(X\theta)) - (1-y^T)log(1-sigmoid(X\theta)))

Code in Octave to compute cost function

J = (1/m) * ( -y' * log(sigmoid(X*theta) ) - (1-y') * log(1-sigmoid(X*theta)) );

We need to get the parameter $\theta$ where $J${(\theta)} is min. Then we can make a prediction when given new $x$ using
$h_{\theta }\left(x\right)=\frac{1}{1+e^{-{\theta }^{T}X}}$
h\theta(x) = \frac{1}{1 + e^{-\theta^TX}}

3. Gradient Descent algorithm

Using Gradient Descent to find value of $\theta$ when $J_{(\theta)}$ is min, we have

Repeat until convergence
${\theta }_j:={\theta }_j-\alpha \frac{\mathrm{\partial }}{\mathrm{\partial }{\theta }_j}J\left(\theta \right)$
\theta_j := \theta_j - \alpha \frac {\partial }{\partial \theta_j}J(\theta)

Repeat until convergence
${\theta }_j:={\theta }_j-\alpha \frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})x^{\left(i\right)}$
\theta_j := \thetaj - \alpha \frac{1}{m} \sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) x^{\left(i\right)}

Vectorized form:
$\theta :=\theta -\frac{\alpha }{m}\left(X^T\right(sigmoid\left(X\theta \right)-\vec{y}\left)\right)$
\theta := \theta - \frac{\alpha}{m} \left( X^T (sigmoid(X\theta) - \vec{y}) \right)

Code in Octave to compute gradient step $\frac {\partial }{\partial \theta_j}J(\theta)$

grad = (1 / m) * (X' * (sigmoid( X * theta) - y) );

4. Adding Regularization parameter

Regularized cost function:
$J_{\left(\theta \right)}=-\frac{1}{m}\left[{\sum }_{i=1}^m{y}^{\left(i\right)}log\right(h_{\theta }\left(x^{\left(i\right)}\right)+(1-y^{\left(i\right)})log(1-h_{\theta }(x^{\left(i\right)}\left)\right)]+\frac{\lambda }{2m}{\sum }_{j=1}^n{\theta }_j^2$
J{(\theta)} = -\frac{1}{m}\left[ \sum{i=1}^{m} y^{(i)} log(h\theta(x^{(i)}) + (1-y^{(i)})log(1 - h\theta(x^{(i)}))\right] + \frac{\lambda}{2m}\sum_{j=1}^{n}\theta_j^2

The second sum, $\sum_{j=1}^{n}\theta_j^2$ means to explicitly exclude the bias term, $\theta_0$. I.e. the $\theta$ vector is indexed from 0 to n (holding n+1 values, $\theta_0$ through $\theta_n$), and this sum explicitly skips $\theta_0$, by running from 1 to n, skipping 0.

Octave code to compute cost function with regularization

J = (1/m) * (-y' * log(sigmoid(X*theta)) - (1-y')*log(1-sigmoid(X*theta))) + lambda/(2*m)*sum(theta(2:end).^2);

Thus, when computing the equation, we should continuously update the two following equations:
Regularized Gradient Descent:
Repeat
{
$\begin{array}{cc}{\theta }_0& :={\theta }_0-\alpha \frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})x_0^{\left(i\right)}\\ {\theta }_j& :={\theta }_j-\alpha [\left(\frac{1}{m}{\sum }_{i=1}^m\left(h_{\theta }\right(x^{\left(i\right)})-y^{\left(i\right)})x^{\left(i\right)}\right)+\frac{\lambda }{m}{\theta }_j]\text{<mi mathvariant="normal">f</mi><mi mathvariant="normal">o</mi><mi mathvariant="normal">r</mi>}j\ge 1\end{array}$
\begin{aligned}
\theta_0 &:= \theta0 - \alpha \frac{1}{m} \sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) x_0^{\left(i\right)} \
\theta_j &:= \thetaj - \alpha \left[ \left(\frac{1}{m} \sum{i=1}^{m} \left( h_\theta ( x^{(i)} ) - y^{(i)} \right) x^{\left(i\right)} \right) + \frac{\lambda}{m}\theta_j \right] \quad \textrm{for} \quad j \geq 1
\end{aligned}

}

Octave code to compute gradient step $\frac {\partial }{\partial \theta_j}J(\theta)$

grad = (1 / m) * (X' * (sigmoid( X * theta) - y)) + (lambda/m)*[0; theta(2:end)];

Notice that we don’t add the regularization term for $\theta_0$

5. Advanced Optimization

Prepare a function that can compute $J_{(\theta)}$ and $\frac {\partial }{\partial \theta_j}J(\theta)$ for a given $\theta$

function [jVal, gradient] = costFunction(theta)
  jVal = [...code to compute J(theta)...];
  gradient = [...code to compute derivative of J(theta)...];
end

Then with this function Octave can provide us some advanced algorithms to compute min of $J_{(\theta)}$. We should not implement these below algorithms by ourselves.

• Conjugate gradient
• BFGS
• L-BFGS

options = optimset('GradObj', 'on', 'MaxIter', 100);
initialTheta = zeros(2,1);
[optTheta, functionVal, exitFlag] = fminunc(@costFunction, initialTheta, options);

We give to the function fminunc() our cost function, our initial vector of theta values, and the options object that we created beforehand.

Advantages:
No need to pick up $\alpha$.
Often faster than gradient descent.

Disadvantages:
More complex.
Practical advice: try a couple of different libraries.